Boost.Graphでの最短経路探索

先日、Boost.勉強会 #14 東京に参加させて頂いたが、そこでBoost.Graphの話があった。
復習がてら、今回はTDD Boot Camp 東京 for C++での最短経路探索の課題(TDD Boot Camp 東京 for C++ 課題)をBoost.Graphで解いてみる。なお課題は規模が大きいので、今回は横浜近辺の5駅に絞った。

グラフ構造の構築

まずBoost.Graphでグラフ構造を記述する。
なおBoost.Graphはgraphvizのグラフ図を出力できるので、今回は記述したグラフ構造をgraphvizで画像化して視覚的に確認する。コードは以下。

#include <iostream>
#include <vector>
#include <boost/graph/adjacency_list.hpp>
#include <fstream>
#include <boost/graph/graphviz.hpp>

using namespace boost;

typedef adjacency_list<listS, vecS, undirectedS, no_property, property<edge_weight_t, int>> Graph;
typedef std::pair<int, int> Edge;
typedef graph_traits<Graph>::vertex_descriptor Vertex;

//駅の定義
enum {
    Yokohama, 
    MusashiKosugi, 
    Kawasaki, 
    Shibuya, 
    Tokyo, 
    N
};

const char* NameList[] = {
    "Yokohama",
    "MusashiKosugi",
    "Kawasaki",
    "Shibuya",
    "Tokyo"
};

int main()
{
    //経路と所要時間の定義
    const std::vector<Edge> edges = {
        {Yokohama, MusashiKosugi}, 
        {Yokohama, Kawasaki},
        {MusashiKosugi, Kawasaki},
        {MusashiKosugi, Shibuya},
        {Kawasaki, Tokyo},
        {Shibuya, Tokyo}
    };

    const std::vector<int> weights = { 
        23,
        14,
        19,
        21,
        24,
        25
    };
    
    const Graph g(edges.begin(), edges.end(), weights.begin(), N);

    std::ofstream file("trainpath.dot");
    write_graphviz(file, g, make_label_writer(NameList));
    return 0;
}

上記のコードを実行した後、生成されたgraphvizのdotファイルを「dot -Tpng trainpath.dot -o trainpath.png」などのコマンドでpngに変換する。すると以下の様な画像が得られる。

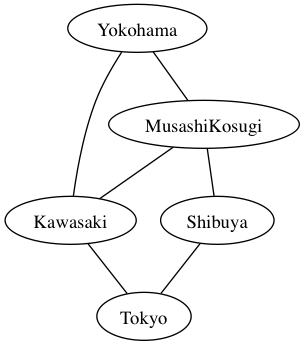
最短経路検索

グラフ構造を記述できたら、今回は横浜・東京間の最短経路をダイクストラ法を使って導き出す。
コードは以下。

#include <iostream>
#include <vector>
#include <deque>
#include <boost/graph/adjacency_list.hpp>
#include <boost/graph/dijkstra_shortest_paths.hpp>

using namespace boost;

typedef adjacency_list<listS, vecS, undirectedS, no_property, property<edge_weight_t, int>> Graph;
typedef std::pair<int, int> Edge;
typedef graph_traits<Graph>::vertex_descriptor Vertex;

//駅の定義
enum {
    Yokohama, 
    MusashiKosugi, 
    Kawasaki, 
    Shibuya, 
    Tokyo, 
    N
};
const char* NameList[] = {
    "Yokohama",
    "MusashiKosugi",
    "Kawasaki",
    "Shibuya",
    "Tokyo"
};

int main()
{
    //経路と所要時間
    const std::vector<Edge> edges = {
        {Yokohama, MusashiKosugi}, 
        {Yokohama, Kawasaki},
        {MusashiKosugi, Kawasaki},
        {MusashiKosugi, Shibuya},
        {Kawasaki, Tokyo},
        {Shibuya, Tokyo}
    };
    const std::vector<int> weights = { 
        23,
        14,
        19,
        21,
        24,
        25
    };
    
    //最短経路の探索
    const Graph g(edges.begin(), edges.end(), weights.begin(), N);
    const Vertex from = Yokohama;
    const Vertex to = Tokyo;

    std::vector<Vertex> parents(num_vertices(g));
    std::vector<std::size_t> distance(num_vertices(g));
    dijkstra_shortest_paths(g, from, predecessor_map(&parents[0]).distance_map(&distance[0]));

    //探索結果をリスト化
    std::deque<Vertex> route;
    for (Vertex v = to; v != from; v = parents[v])
    {
        route.push_front(v);
    }
    route.push_front(from);
    for (const Vertex v : route)
    {
        std::cout << NameList[v] << std::endl;
    }
    return 0; 
}

これを実行すると最短経路が以下のようにリストアップされる。

Yokohama
Kawasaki
Tokyo

また最短経路の時間は、上記のコードの場合distance[to]に格納されている。また今回はグラフ構造が自明だったため今回は省いているけれど、経路が存在しないことは「parents[to] == to」が真となることの確認で判定できる。