Pythonでのやや複雑な単回帰分析について。今回は書籍「データ指向のソフトウェア品質マネジメント」を題材にやってみる。Pythonでの記述は*を参考にした
分析データとしては、書籍での「テスト工程での不具合検出数の予測」にて提供されているCSVデータを「data.csv」に保存して使用する。
分析内容
分析では、不具合検出に関わるデータの相関性を評価して、不具合数の予測に使える回帰モデルを構築することを目指している。
データの俯瞰と相関性の評価
まずデータを俯瞰した上で、分析対象とするFailures(障害数)とKLOC(テスト対象規模)の相関を評価する。
●グラフ化
グラフで全体の傾向を主観的に把握する。
スクリプト
# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt
import pandas as pd
prj_data = pd.read_csv("data.csv", sep="\t")
# 使用しない行を削除
del prj_data['Prj']
# 欠損を削除
prj_data = prj_data.dropna()
# 散布図で見る
plt.scatter(prj_data['Failures'], prj_data['KLOC'])
plt.show()
# ヒストグラムで見る
plt.figure()
plt.hist(prj_data["Failures"])
plt.xlabel("Failures")
plt.ylabel("Number")
plt.show()
出力
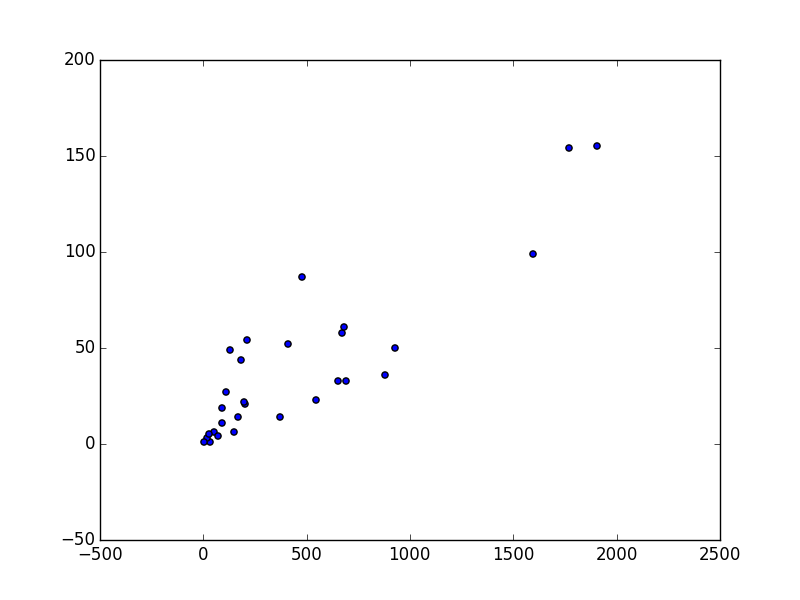
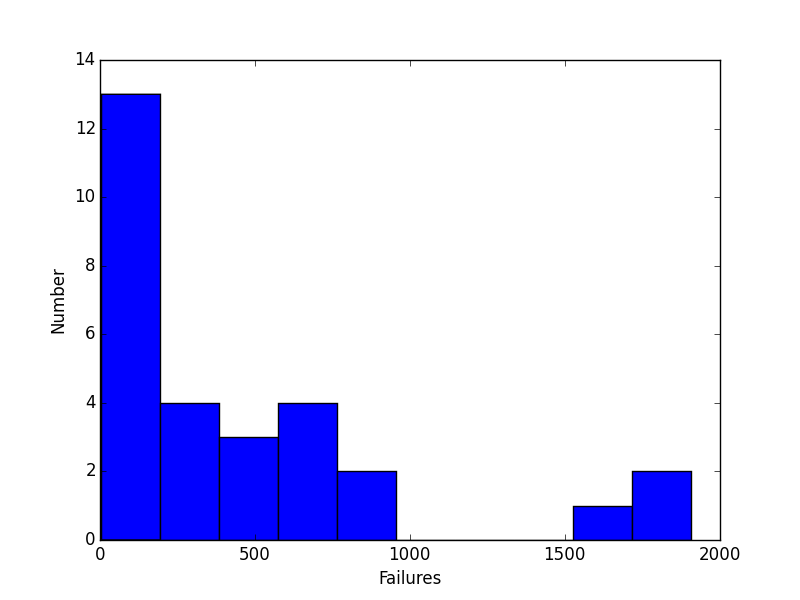
●相関係数の評価
相関係数を評価して、正の相関があることを確認する。
スクリプト
〜上の続き〜 print prj_data.corr()
出力
Failures KLOC Failures 1.000000 0.883083 KLOC 0.883083 1.000000
単回帰分析
回帰分析ではデータの分布から推測して、対数を用いた以下のモデルを用いる。
log (Failures) = X * log(KLOC) + Y
対数が含まれるため、文字列で回帰モデルを簡単に記述できるstatsmodelsを使用する。
スクリプト
# -*- coding: utf-8 -*-
import pandas as pd
import numpy as np
import statsmodels.formula.api as sm
prj_data = pd.read_csv("data.csv", sep="\t")
del prj_data['Prj']
prj_data = prj_data.dropna()
result = sm.ols(formula="np.log(Failures) ~ np.log(KLOC)", data=prj_data).fit()
# 概要だけ
print result.params
# 分析データ含めて表示
print result.summary()
出力(paramsの表示)
題材の書籍と概ね同じ値を出力できている。
Intercept 2.460562 np.log(KLOC) 0.956357 dtype: float64
出力(summaryの表示)
P値、R-squaredの値を含め、題材書籍と同じ分析結果になっており、概ね適用可能な回帰モデルとなっていると判断できる。
OLS Regression Results
==============================================================================
Dep. Variable: np.log(Failures) R-squared: 0.779
Model: OLS Adj. R-squared: 0.771
Method: Least Squares F-statistic: 95.38
Date: Wed, 04 Mar 2015 Prob (F-statistic): 2.35e-10
Time: 01:40:49 Log-Likelihood: -29.481
No. Observations: 29 AIC: 62.96
Df Residuals: 27 BIC: 65.70
Df Model: 1
Covariance Type: nonrobust
================================================================================
coef std err t P>|t| [95.0% Conf. Int.]
--------------------------------------------------------------------------------
Intercept 2.4606 0.325 7.578 0.000 1.794 3.127
np.log(KLOC) 0.9564 0.098 9.766 0.000 0.755 1.157
==============================================================================
Omnibus: 5.037 Durbin-Watson: 2.194
Prob(Omnibus): 0.081 Jarque-Bera (JB): 1.856
Skew: -0.181 Prob(JB): 0.395
Kurtosis: 1.815 Cond. No. 9.02
==============================================================================